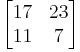Monge array
In computer science, Monge arrays, or Monge matrices, are mathematical objects named for their discoverer, the French mathematician Gaspard Monge.
An m-by-n matrix is said to be a Monge array if, for all 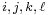 such that
such that
one obtains
So whenever we pick two rows and two columns of a Monge array (a 2 × 2 sub-matrix) and consider the four elements at the intersection points, the sum of the upper-left and lower right elements (across the main diagonal) is less than or equal to the sum of the lower-left and upper-right elements (across the antidiagonal).
This matrix is a Monge array:
For example, take the intersection of rows 2 and 4 with columns 1 and 5. The four elements are:
- 17 + 7 = 24
- 23 + 11 = 34
The sum of the upper-left and lower right elements is less than or equal to the sum of the lower-left and upper-right elements.
Contents |
Properties
- The above definition is equivalent to the statement
- A matrix is a Monge array if and only if
![A[i,j] %2B A[i%2B1,j%2B1]\le A[i,j%2B1] %2B A[i%2B1,j]](/2012-wikipedia_en_all_nopic_01_2012/I/0e53917f95b82e0b508d89a8376d28fd.png) for all
for all 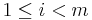 and
and 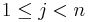 .
.
- Any subarray produced by selecting certain rows and columns from an original Monge array will itself be a Monge array.
- Any linear combination with non-negative coefficients of Monge arrays is itself a Monge array.
- One interesting property of Monge arrays is that if you mark with a circle the leftmost minimum of each row, you will discover that your circles march downward to the right; that is to say, if
![f(x) = \min_{i\in 1\ldots m} A[i,x]](/2012-wikipedia_en_all_nopic_01_2012/I/826c3d5d2665d4eb674ec8d703b5fdcd.png) , then
, then 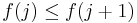 for all
for all 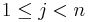 . Symmetrically, if you mark the uppermost minimum of each column, your circles will march rightwards and downwards. The row and column maxima march in the opposite direction: upwards to the right and downwards to the left.
. Symmetrically, if you mark the uppermost minimum of each column, your circles will march rightwards and downwards. The row and column maxima march in the opposite direction: upwards to the right and downwards to the left.
- The notion of weak Monge arrays has been proposed; a weak Monge array is a square n-by-n matrix which satisfies the Monge property
![A[i,i] %2B A[r,s]\le A[i,s] %2B A[r,i]](/2012-wikipedia_en_all_nopic_01_2012/I/83a7bdb9828bcc444f2fe5e017b98ae4.png) only for all
only for all 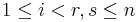 .
.
Applications
- A square Monge matrix which is also symmetric about its main diagonal is called a Supnick matrix (after Fred Supnick); this kind of matrix has applications to the traveling salesman problem (namely, that the problem admits of easy solutions when the distance matrix can be written as a Supnick matrix). Note that any linear combination of Supnick matrices is itself a Supnick matrix.
Bibliography
- 'Some problems around travelling salesmen, dart boards, and euro-coins' by Vladimir G. Deineko and Gerhard J. Woeginger, appeared in the Bulletin of the European Association for Theoretical Computer Science (EATCS), Number 90, October 2006, ISSN 0252-9742, page 44. See online edition (PDF).
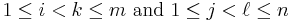
![A[i,j] %2B A[k,\ell] \le A[i,\ell] %2B A[k,j].\,](/2012-wikipedia_en_all_nopic_01_2012/I/acee0a505fa26f17301a46da794a1615.png)